MultiPy

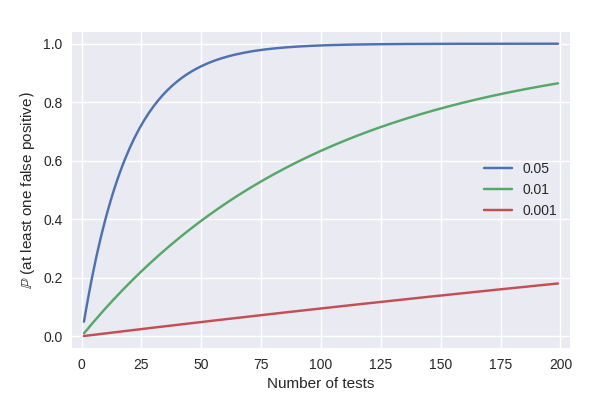
Testing multiple hypotheses simultaneously increases the number of false positive findings if the corresponding p-values are not corrected. While this multiple testing problem is well known, the classic and advanced correction methods are yet to be implemented into a coherent Python package. This package sets out to fill this gap by implementing methods for controlling the family-wise error rate (FWER) and the false discovery rate (FDR).

News

• A paper of the software is now published in the Journal of Neuroscience Methods (13th March 2020)

• A new pre-print of the software is now available on BioRxiv (11th September 2019)

• MultiPy is presented as a poster in the MEG Nord conference at Jyväskylä, Finland (8–10th May 2019)

• MultiPy is presented in a neuroscience seminar at the Jyväskylä Centre for Interdisciplinary Brain Research, Jyväskylä, Finland (30th November 2018)

• MultiPy is presented in the Tool of the month seminar at the University of Helsinki, Finland (30th May 2018)

• MultiPy is presented as a poster in the Neuronal circuit dynamics across scales and species symposium at Helsinki, Finland (3–4th May 2018)

Installation

Install the software manually to get the latest version. The pip version is updated approximately every two or three months.

Using pip

pip install multipy

Manually

git clone https://github.com/puolival/multipy.git
cd multipy/
ipython setup.py install

Dependencies

The required packages are NumPy (version 1.10.2 or later), SciPy (version 0.17.0 or later), Matplotlib (version 2.1.0 or later), Seaborn (version 0.8.0 or later), and scikit-image (version 0.13.0 or later). The program codes also probably work with recent earlier versions of these packages but this has not been tested.

Problems or suggestions?

Please open an issue if you find a bug or have an idea how the software could be improved.

Methods for controlling the FWER

• Bonferroni correction
• Šidák correction [1]
• Hochberg’s procedure [2]
• Holm-Bonferroni procedure [3]
• Permutation tests [8, 10]
• Random field theory (RFT) based approaches [9, 11]

Quick example

from multipy.data import neuhaus
from multipy.fwer import sidak

pvals = neuhaus()
significant_pvals = sidak(pvals, alpha=0.05)
print(zip(['{:.4f}'.format(p) for p in pvals], significant_pvals))

[('0.0001',  True), ('0.0004',  True), ('0.0019',  True), ('0.0095', False), ('0.0201', False), 
 ('0.0278', False), ('0.0298', False), ('0.0344', False), ('0.0459', False), ('0.3240', False), 
 ('0.4262', False), ('0.5719', False), ('0.6528', False), ('0.7590', False), ('1.0000', False)]

Methods for controlling the FDR

• Benjamini-Hochberg procedure (the classic FDR procedure) [4]
• Storey-Tibshirani q-value procedure [5]
• Adaptive linear step-up procedure [6–7]
• Two-stage linear step-up procedure [7]

Quick example

from multipy.fdr import lsu
from multipy.data import neuhaus

pvals = neuhaus()
significant_pvals = lsu(pvals, q=0.05)
print(zip(['{:.4f}'.format(p) for p in pvals], significant_pvals))

[('0.0001',  True), ('0.0004',  True), ('0.0019',  True), ('0.0095',  True), ('0.0201', False), 
 ('0.0278', False), ('0.0298', False), ('0.0344', False), ('0.0459', False), ('0.3240', False), 
 ('0.4262', False), ('0.5719', False), ('0.6528', False), ('0.7590', False), ('1.0000', False)]

Covariate-adjusted methods

• Independent hypothesis weighting (IHW) [17]

Data and models

• Spatial two-group model [12]
• Spatial separate-classes model. Partly based on [12–13].

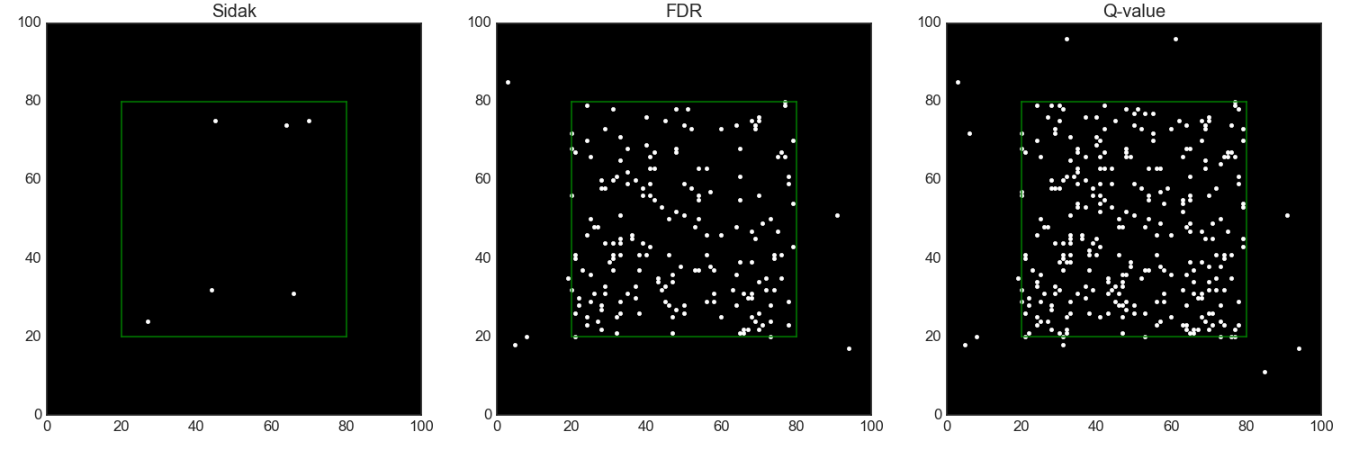
There is a true effect at each location within the green box and no true effects outside.

Methods for reproducibility analyses

• The partial conjuction method
• The FWER replicability method [14–16]
• The FDR r-value method [18]

Data visualization

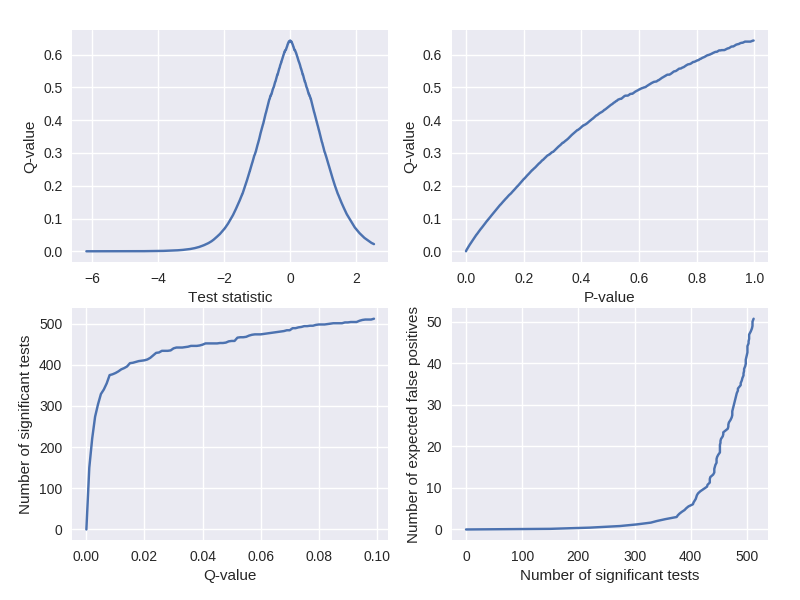
Quick example

Visualize q-values similar to Storey and Tibshirani (2003).

from multipy.data import two_group_model
from multipy.fdr import qvalue
from multipy.viz import plot_qvalue_diagnostics

tstats, pvals = two_group_model(N=25, m=1000, pi0=0.5, delta=1)
_, qvals = qvalue(pvals)
plot_qvalue_diagnostics(tstats, pvals, qvals)

Citation

Puoliväli T, Palva S, Palva JM (2020): Influence of multiple hypothesis testing on reproducibility in neuroimaging research: A simulation study and Python-based software. Journal of Neuroscience Methods 337:108654.

A pre-print of the manuscript is available on BioRxiv.

Poster presentations:

Puoliväli T, Palva S, Palva JM (2019): MultiPy: Multiple hypothesis testing in Python. MEG Nord, Jyväskylä, Finland, 8–10th May.

Puoliväli T, Lobier M, Palva S, Palva JM (2018): MultiPy: Multiple hypothesis testing in Python. Neuronal Circuit Dynamics across Scales and Species, Helsinki, Finland, 3–4th May.

References

[1] Sidak Z (1967): Confidence regions for the means of multivariate normal distributions. Journal of the American Statistical Association 62(318):626–633.

[2] Hochberg Y (1988): A sharper Bonferroni procedure for multiple tests of significance. Biometrika 75(4):800–802.

[3] Holm S (1979): A simple sequentially rejective multiple test procedure. Scandinavian Journal of Statistics 6(2):65–70.

[4] Benjamini Y, Hochberg Y (1995): Controlling the false discovery rate: A practical and powerful approach to multiple testing. Journal of Royal Statistical Society. Series B (Methodological): 57(1):289–300.

[5] Storey JD, Tibshirani R (2003): Statistical significance for genomewide studies. The Proceedings of the National Academy of the United States of America 100(16):9440–9445.

[6] Benjamini Y, Hochberg Y (2000): On the adaptive control of the false discovery rate in multiple testing with independent statistics. Journal of Educational and Behavioral Statistics 25:60–83.

[7] Benjamini Y, Krieger AM, Yekutieli D (2006): Adaptive linear step-up procedures that control the false discovery rate. Biometrika 93(3):491–507.

[8] Maris E, Oostenveld R (2007): Nonparametric statistical testing of EEG- and MEG-data. Journal of Neuroscience Methods 164(1):177–190.

[9] Brett M, Penny W, Kiebel S (2003): An introduction to random field theory. Human Brain Function (2nd edition). [full text]

[10] Phipson B, Smyth GK (2010): Permutation p-values should never be zero: Calculating exact p-values when permutations are randomly drawn. Statistical Applications in Genetics and Molecular Biology 9:article39.

[11] Worsley KJ, Evans AC, Marrett S, Neelin P (1992): A three-dimensional statistical analysis for CBF activation studies in human brain. Journal of Cerebral Blood Flow and Metabolism 12:900–918.

[12] Bennett CM, Wolford GL, Miller MB (2009): The principled control of false positives in neuroimaging. Social Cognitive and Affective Neuroscience 4(4):417–422.

[13] Efron B (2008): Simultaneous inference: When should hypothesis testing problems be combined? The Annals of Applied Statistics 2(1):197–223.

[14] Benjamini Y, Heller R (2008): Screening for partial conjuction hypotheses. Biometrics 64:1215–1222.

[15] Benjamini Y, Heller Y, Yekutieli D (2009): Selective inference in complex research. Philosophical Transactions of the Royal Society A 367:4255–4271.

[16] Bogomolov M, Heller R (2013): Discovering findings that replicate from a primary study high dimension to a follow-up study. Journal of the American Statistical Association 108(504):1480–1492.

[17] Ignatiadis N, Klaus B, Zaugg JB, Huber W (2016): Data-driven hypothesis weighting increases detection power in genome-scale multiple testing. Nature Methods 13:577–580.

[18] Heller R, Bogomolov M, Benjamini Y (2014): Deciding whether follow-up studies have replicated findings in a preliminary large-scale omics study. The Proceedings of the National Academy of Sciences of the United States of America 111(46):16262–16267.